드롭아웃 짱짱맨!

사족

NLP 관련 논문을 하나씩 차근차근 보기 위해서 BERT를 내에 사용되는 Trasfomer를 공부해야하나 하다가 그럼 그 안에 있는 중요한 이론인 Attention을 봐야겠군 하고 Attention을 켜니 Seq2Seq가 맞이하고 있었고, 이 Seq2Seq를 이해하기 위해서는 RNN을 알아야하기 때문에 RNN 논문부터 파헤치기로 했다.

RNN의 일종에는 LSTM와 GLU 등이 있었고, LSTM을 먼저 공부하기 위해서 찾아본 논문 중, 이 논문이 쉬워보여서 가장 먼저 읽어보았다(사실 LSTM에 대한 설명인 줄 알았는데 LSTM에서 좀 더 정확도를 올리기 위한 꿀팁! 같은 내용이어서 이 이후에는 LSTM에 대해서 공부를 해볼 생각이다.)

세 줄 요약하자면

1. RNN의 일종인 LSTM에 Dropout을 어떻게 적용하느냐에 따라서 좋은 결과를 보일 수도 있다는 논문이다.
2. 요점은 순환 유닛에 드롭아웃 연산을 적용하면 중요한 메모리에 혼란이 올 수 있어 좋은 결과를 얻지 못한다.
3. 그러니 비순환 유닛에만 드롭아웃 연산을 적용하자! 였다.

Abstract

• Long Short-Term Memory(LSTM) 유닛과 함께 RNN을 위한 간단한 정규화 테크닉을 소개.
• Dropout은 뉴럴 네트워크를 정규화하는데 있어서 가장 성공적인 테크닉이지만 RNNs와 LSTMs에서는 잘 작동하지 않았다.
• 이 논문에서는 LSTMs에서 Dropout을 어떻게 하면 정확하게 적용할 수 있는지(correctly apply), 그리고 이 기법을 사용하면 다양한 작업들(언어모델(LM), 음성 인식, 이미지 캡션 생성, 기계 번역)에서의 오버피팅을 대체적으로 감소시켜주는 것을 보여준다.

Introduction

• RNN은 언어 모델, 음성 인식, 기계 번역을 포함해서 중요한 작업들에서 state of the art 성능을 달성한 뉴럴 시퀀스 모델이다.
• 뉴럴 네트워크에 성공적인 적용은 좋은 정규화가 요구된다고 알려져있다.
• 피드 포워드 네트워크에서 가장 파워풀한 정규화 방법인 Dropout이 RNNs에서 잘 작동하지 않았고 이에 대한 결과로 RNNs의 실용적인 응용은 종종 너무 작은 모델을 사용했다 -> 너무 큰 RNN 모델은 오버피팅하는 경향이 있었기 때문
• 존재하는 정규화 방법들은 RNN을 상대적으로 작은 향상만을 줬다.
• 그래서 우리는 드롭아웃을 정확하게 사용했을 때 LSTMs에서 오버피팅을 많이(greatly) 감소시킬 수 있다는 것을 보여줄 것.

Regularizing RNNs With LSTM Cells

• 섹션 a에서는 deep LSTM에 대해서 설명
• 섹션 b에서는 어떻게 정규화하는지, 그리고 왜 우리의 정규화 작업이 잘 되는지에 대한 설명

a. Long-Short Term Memory Units

• RNN 역학은 이전으로부터 현재 은닉 상태로의 결정론적 전환(deterministic transitions)을 사용해 설명할 수 있음.
• 이게 결정론적 상태 전환 함수(The deterministic state transition function)

\[\text{RNN: }h^{l-1}_t, h^{l}_{t-1} \rightarrow h^{l}_{t}\]

• 전통적인 RNNs에서 이 함수는 이렇게 주어진다.

\[h^{l}_{t} = f(T_{n,n}h^{l-1}_t + T_{n,n}h^{l}_{t-1}), \text{where} f \in \{\text{sigm, tanh}\}\]

• LSTM은 복잡한 역학관계가 있어 많은 수의 타임 스텝에 대한 정보를 쉽게 기억할 수 있다.
• ‘long term’ 메모리는 메모리 셀의 벡터 안에 저장된다($C^l_t \in \mathbb{R}^n$).
• 비록 연결 구조와 활성화 함수에 차이가 많은 LSTM 아키텍처지만, 모든 LSTM 아키텍처는 긴 시간 동안의 정보를 저장하는 명시적 메모리 셀을 가지고 있다.
• LSTM은 메모리셀을 덮어쓰거나 회수하거나 다음 타임 스텝에 유지할지에 대해서 결정할 수 있다.
• 실험에 사용된 LSTM 아키텍처는 다음 공식을 사용.

\[\text{LSTM} : h^{l-1}_{t}, h^{l}_{t-1}, c^{l}_{t-1} \rightarrow h^l_t, c^l_t\] \[\begin{pmatrix} i \\ f \\ o \\ g \end{pmatrix} = \begin{pmatrix} sigm \\ sigm \\ sigm \\ sigm \end{pmatrix} T_{2n, 4n} \begin{pmatrix} h^{l-1}_t \\ h^l_{t-1} \end{pmatrix}\] \[c^l_t = f \bigodot c^l_{t-1} + i \bigodot g\] \[h^l_t = o \bigodot tanh(c^l_t)\]

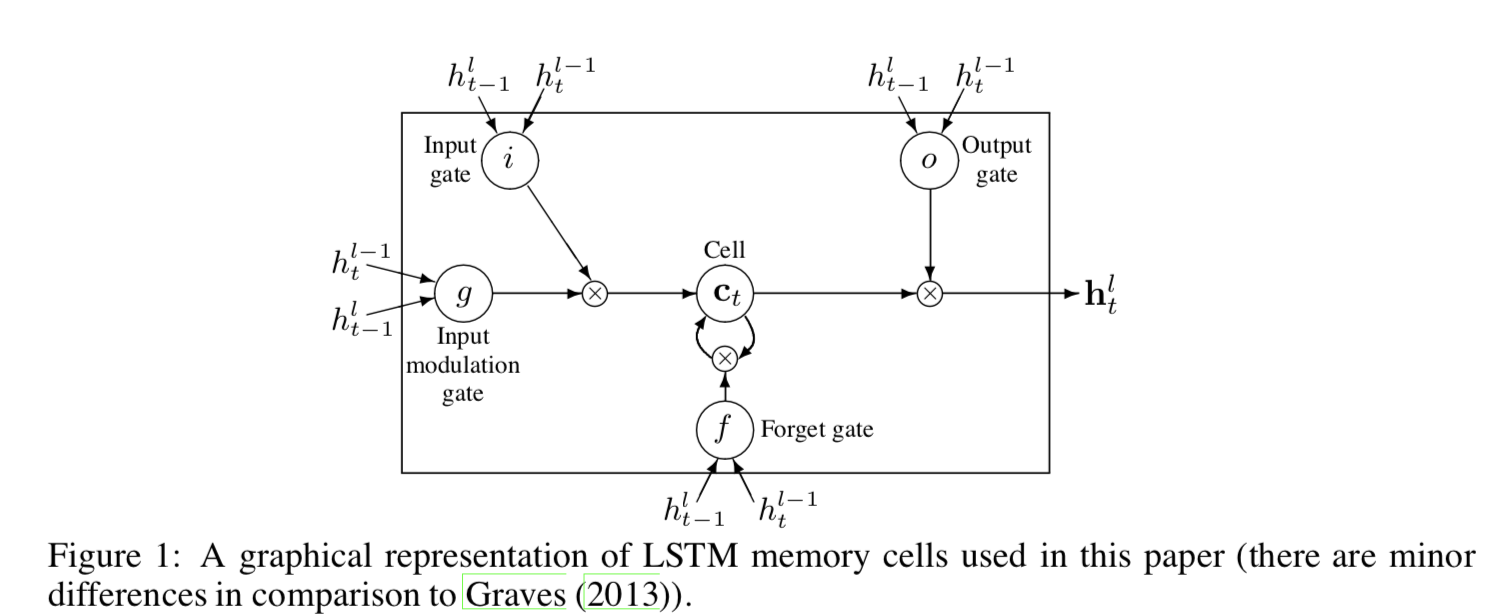
• 이 공식에서, 시그모이드(sigm)와 tanh은 원소별(element-wise) 계산 적용이다. Figure 1은 LSTM 공식을 보여준다.

b. Regularization With Dropout

• LSTM에 드롭아웃을 적용해 성공적으로 오버피팅을 감소시키는 방법이 이 논문의 핵심!
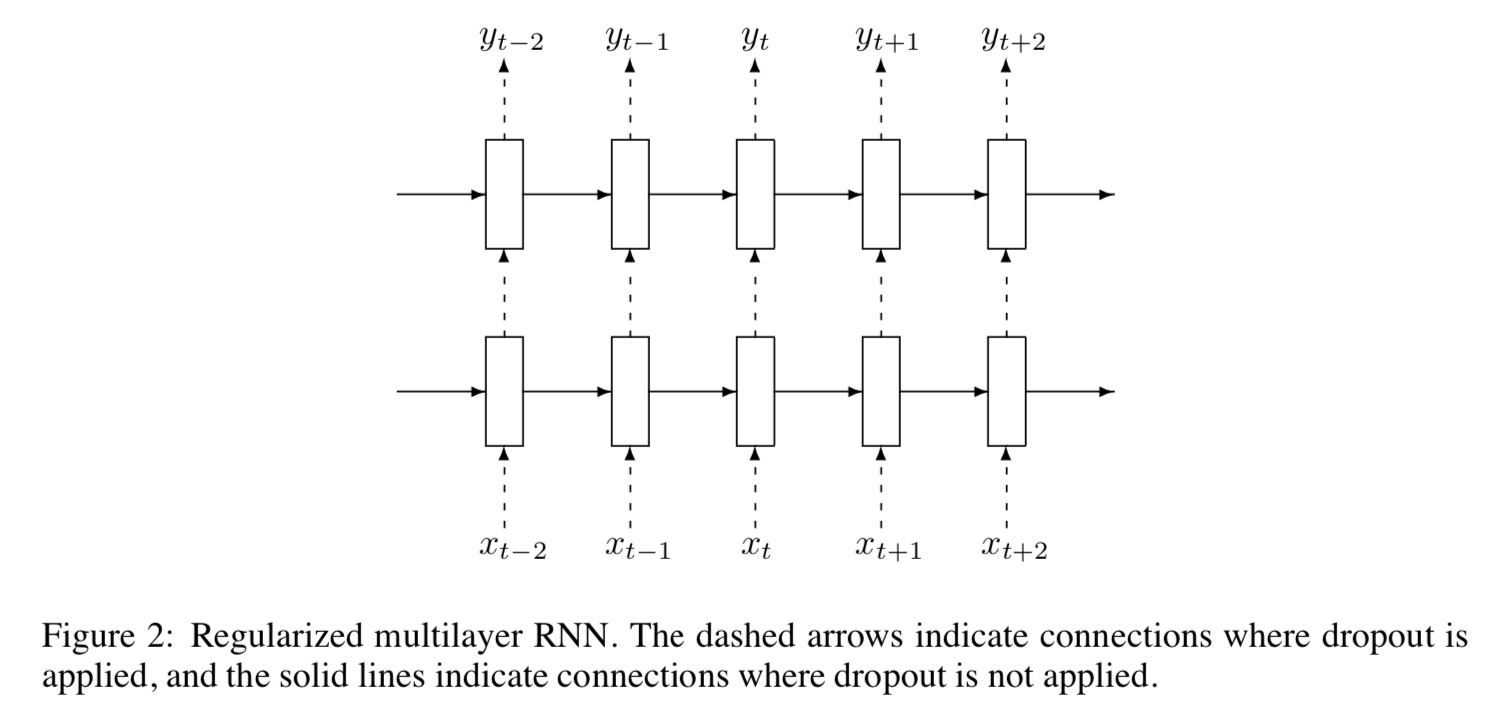
• 핵심 아이디어는 드롭아웃 연산을 비순환 연결에만 적용하는 것
• 여기서 D는 인수의 임의 부분 집합을 0으로 설정하는 드롭아웃 연산자.

\[\begin{pmatrix} i \\ f \\ o \\ g \end{pmatrix} = \begin{pmatrix} sigm \\ sigm \\ sigm \\ sigm \end{pmatrix} T_{2n, 4n} \begin{pmatrix} D(h^{l-1}_t) \\ h^l_{t-1} \end{pmatrix}\] \[c^l_t = f \bigodot c^l_{t-1} + i \bigodot g\] \[h^l_t = o \bigodot tanh(c^l_t)\]

• 드롭아웃 연산자는 유닛이 운반하는 정보를 변형(corrupt)시키며, 그들의 중간 연산을 더 강력하게(robustly) 수행하도록 한다(forcing them to perform) -> force라는 단어를 사용한 것으로 보아 강제로 하게하는 느낌인 것 같다.
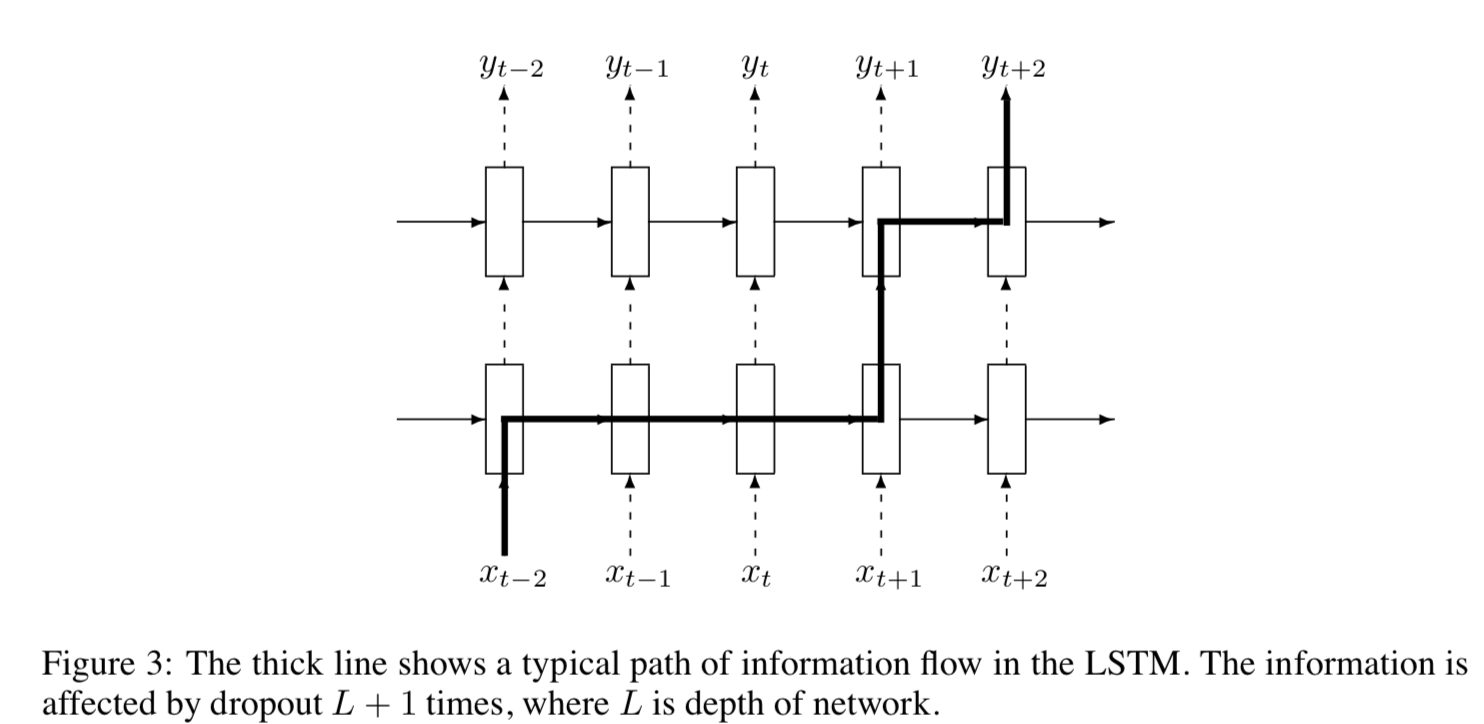
• 동시에, 유닛들의 모든 정보가 지워지는 것을 원하지 않는다. -> 유닛들은 과거의 많은 타임 스텝에서 발생된 이벤트를 기억하는 것이 특히 중요하다. figure 3에서는 어떻게 정보가 타임스텝 t-2에서 발생한 사건에서 우리의 드롭아웃 구현 내에 있는 시간 스탭 t+2의 예측으로 흐를 수 있는지를 보여준다.
• 정보가 드롭아웃 연산에 의해 정확하게 L+1 시간에 변형된다는 것을 볼 수 있고, 이 숫자는 정보가 횡단한 타임스텝의 수와 독립적이다.
• 일반적인 드롭아웃은 순환 연결에 혼란을 주는데(perturb) 이것이 LSTM이 장기간 저장된 정보를 학습하는데 어렵게 만든다.
• 순환 연결에 드롭아웃을 사용하지 않음으로써 LSTM은 가치있는 기억 능력(valuable memorization ability) 희생 없이 드롭아웃 정규화에서 이익을 얻을 수 있다.

Conclusion

• LSTM에 드롭아웃을 적용하는 간단한 방법을 보여줬으며, 다른 도메인들의 여러 문제들에 대해 잘 해결하는 모습을 보여줬다
• RNNs에 유용한 드롭아웃의 사용으로 드롭아웃이 넓고 다양한 분야에서 퍼포먼스를 향상시킬 수 있다