Attention~

목차

처음으로 이 포스트에 목차라는 걸 넣어본다. 그만큼 쓸 내용이 많다는 것이다.

• 읽기 전에
• 참조한 사이트
• 어텐션
  • 어텐션의 등장 이유
  • 어텐션의 아이디어
  • 어텐션 함수
  • 닷-프로덕트 어텐션

읽기 전에

Transformer에 대해서 공부하기 위해, 논문을 보기 전 Transformer의 근간이 되는 Attention에 대해서 공부한 내용을 요약했다.

참조한 사이트

• 딥 러닝을 이용한 자연어 처리 입문

어텐션

어텐션의 등장 이유

논문 제목 그대로 Transformer는 어텐션(Attention)을 위주로 사용해 구현된 모델이다. 그렇다면 나는 Attention에 대해서 알 필요가 있다고 생각하고, Attention을 먼저 공부했다.

NLP에서 RNN과 LSTM과 같은 모델들은 셀 자체적으로 메모리를 가지게 되면서, 앞 내용을 어느 정도 기억하고 뒷 내용을 보다 잘 예측할 수 있게 해줬다. 하지만 이 또한 두 가지의 고질적인 문제점을 가지고 있다.

1. 정보의 크기가 너무 커버리면 압축하는데 그 만큼 발생하는 정보 손실량이 많아진다.
2. RNN의 고질적인 문제인 기울기 소실(Vanishing Gradient)문제가 발생해버린다.

베니싱 그라디언트!

이를 보정해주기 위해 등장한 기법이 바로 Attention이다.

어텐션의 아이디어

내가 참고했던 사이트에서는 다음과 같이 설명했다.

단순히 이전 t시간에 대한 상태만을 참고하는 RNN과 달리, 어텐션은 매 출력마다 인코더의 전체 입력 문장을 다시 한 번 참고한다. 다만 모든 문장을 전부 동일하게 참고하는 것이 아닌, 좀 더 연관이 있는 단어를 집중(Attention)해서 본다.

이게 무슨 말인가 싶을거다. 뒤에서 설명하겠지만, 디코더의 모든 은닉 상태에서 Softmax를 활용해서 이 비율이 높으면 좀 더 연관이 있다고 본다고 생각하면 된다.

어텐션 함수

어텐션 함수는 다음과 같이 표현된다.

Atention(Q, K, V) = Attention Value

어텐션 함수는 Query에 대해서 모든 Key와의 유사도를 구한다. 그리고 구해낸 이 유사도를 키와 맵핑되어 있는 각각의 Value를 모두 더해서 리턴한다. 여기서 리턴되는 값이 바로 Attention Value다.

Q = Quary: t 시점의 디코더 셀에서의 은닉 상태
K = Keys: 모든 시점의 인코더 셀의 은닉 상태들
V = Values: 모든 시점의 인코더 셀의 은닉 상태들

닷-프로덕트 어텐션

다양한 종류의 어텐션 중, 가장 많이 언급되는 닷-프로덕트 어텐션(Dot-Product Attention)을 적는다. 다른 어텐션들과의 차이는 어떻게 계산하냐의 차이일뿐 메커니즘 자체는 유사하다고 한다.

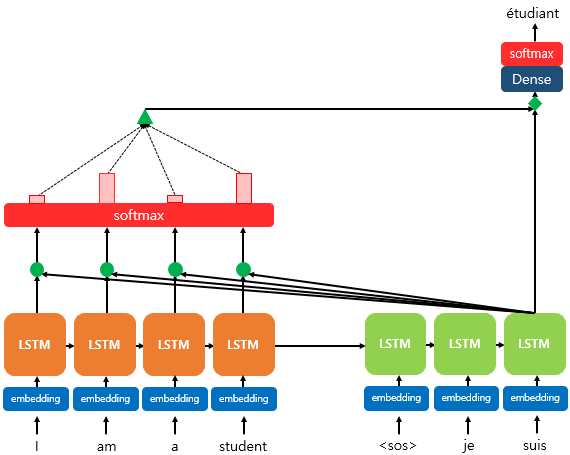
위 그림은 디코더의 세번째 LSTM 셀에서 출력 단어를 예측할 때 어텐션 메커니즘을 사용하는 것을 보여준다.

그림을 간단하게 설명하자면, 디코더의 세번째 LSTM 셀에서 출력 단어를 예측하기 위해서 그 시간의 인코더의 모든 은닉 상태를 다시 한 번 참고한다.

소프트맥스 함수를 통해 나온 결과값은 인코더의 각 단어들이 출력 단어를 예측할 때 얼마나 도움이 되는지를 수치화 한 것인데, 직사각형의 크기가 클 수록 더 도움이 된다는 뜻이다. 이 결과값을 벡터로 담아 디코더로 전송한다.

1) 어텐션 스코어

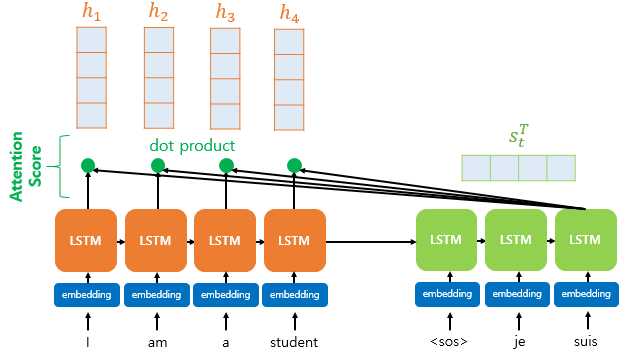
기존 seq2seq에서는 t 시점에서 출력 단어를 예측하기 위해서 t-1 시점의 은닉 상태와 t-1 시점에서 나온 출력 단어가 필요하다. 어텐션 메커니즘은 여기에 어텐션 값(Attention Value)이라는 새로운 값이 필요하다. t번째 단어를 예측하기 위한 어텐션 값을 $a_t$라고 정의한다.

어텐션 값을 구하기 위한 첫번째 스텝은 바로 어텐션 스코어(Attention Score)를 구하는 것이다. 어텐션 스코어는 현재 디코더의 시점 t에서 단어를 예측하기 위해, 인코더의 모든 은닉 상태 값들이 디코더의 현 시점의 은닉 상태 $s_t$와 얼마나 유사한지를 판단하는 스코어 값이다.

닷-프로덕트 어텐션에서는 이 스코어 값을 구하기 위해 $s_t$를 전치(transpose)하고 각 은닉 상태와 내적(dot product)를 수행한다. 즉 모든 어텐션 스코어 값은 스칼라 값이다.

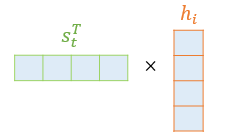
어텐션 스코어 함수를 정의해보면 다음과 같다

\[score(s_{t} \cdot h_{i}) = s^{T}_{t}h_{i}\]

$s_t$ 와 인코더의 모든 은닉 상태의 어텐션 스코어의 모음값을 $e^{t}$라고 정의한다.

\[e^t = [s^{T}_{t}h_{i}, \cdots, s^{T}_{t}h_{N}]\]

2) 소프트맥스(softmax) 함수를 통해 어텐션 분포(Attention Distribution)를 구한다.

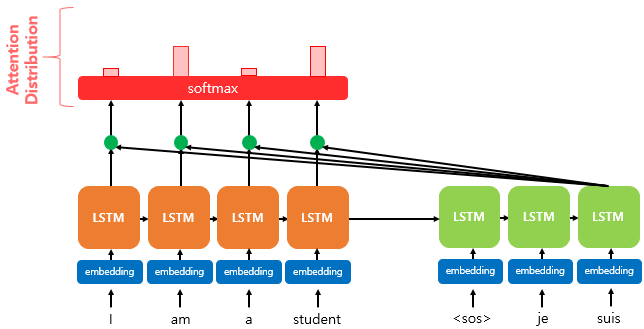
$e^{t}$ 에 소프트맥스 함수를 적용하여, 모든 값을 합하면 1이 되는 확률 분포를 얻어낸다. 이게 어텐션 분포다.

디코더 시점 t에서의 어텐션 가중치의 모음값인 어텐션 분포를 $\alpha^{t}$ 라고 할 때,

\[\alpha^{t} = \text{softmax}(e^t)\]

로 정의할 수 있다.

3) 각 인코더의 어텐션 가중치와 은닉 상태를 가중합하여 어텐션 값(Attention Value)을 구한다.

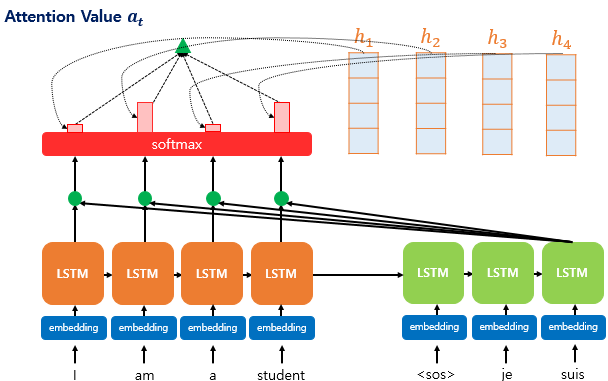
지금까지 구한 값들을 하나로 합치는 단계다. 어텐션의 최종 값을 얻기 위해 각 인코더의 은닉 상태와 어텐션 가중치값들을 곱하고 최종적으로 모두 더한다.

어텐션 함수 출력 값인 어텐션 값(Attention Value) $a_t$ 를 다음의 식으로 구할 수 있다.

\[a_t = \sum^{N}_{i=1}a^{t}_{i}h_{i}\]

이러한 어텐션 값은 종종 인코더의 문맥을 포함하고 있다고 하여, 컨텍스트 벡터라고도 불린다.

4) 어텐션 값과 디코더의 t 시점의 은닉 상태를 연결한다(Concatenate)

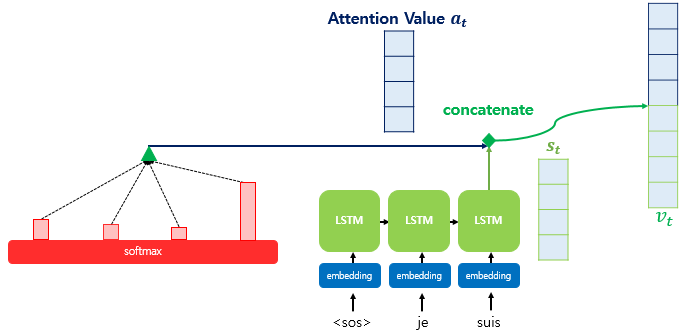
앞서 구한 어텐션 값 $a_t$ 에 $s_t$ 를 결합(Concatenate)해 하나의 벡터로 만드는 작업을 수행한다. 이를 $v_t$ 라고 정의하고, 이 값을 $\hat{y}$ 예측의 연산의 입력으로 사용한다.