뻠블비~

목차

• 읽기 전에
• 참조한 사이트
• 너가 필요한 건 어텐션 뿐이야
• 트랜스포머의 구조
  • 인코더와 디코더
  • 어텐션
    • 스케일드 닷-프로덕트 어텐션
    • 멀티 헤드 어텐션
    • 어텐션 적용
  • 점별 피드포워드 네트워크
  • 임베딩과 소프트맥스
  • 포지셔널 인코딩
• 왜 셀프어텐션?
• 훈련
  • Optimizer
  • 정규화
    • 잔차 드롭아웃
    • 라벨 스무딩
• 결론

읽기 전에

Transformer를 공부하기 이전에 보면 Attention에 대해서 알고 보면 더욱 이해가 쉽다.

NLP에서 State of the art를 달성했던 BERT는 현재 KoBERT, ALBERT 등 성능을 더 끌어올리기 위해 발전시키거나, 모델 사이즈를 줄이는 경량화 작업 등 많은 연구가 진행되고 있다.

이렇게 유명한 모델인 BERT를 공부하기 전에 그 근간이 되는 Transformer를 먼저 공부해보기로 했다.

p.s. 이 글은 논문의 순서를 따라서 작성했다. 이 글 이후에는 트랜스포머를 구현해보는 코드를 업로드할 예정이다.

참조한 사이트

• ‘Attention is All You Need’ 논문
• 해당 논문에 대한 Github
• 딥 러닝을 이용한 자연어 처리 입문
• Attention is all you need paper 뽀개기
• Transformer - Attention Is All You Need 논문 한글 번역

너가 필요한 건 어텐션 뿐이야

논문 제목부터 범상치 않다. 너가 필요한 건 어텐션이 전부야 라는 자신감 넘치는 저 한 문구..

각설하고 지난 Attention, 어텐션 포스트에 기술했듯, 기존의 seq2seq는 고질적인 문제점이 있었고, 이를 보정해주기 위해 어텐션이 사용되었다. 그런데 이 논문은 거기서 멈추지 않고 어텐션만으로 인코더와 디코더를 만들면 어때? 라는 아이디어에서 시작되었다.

트랜스포머의 구조

트랜스포머의 구조는 다음과 같이 되어있다. RNN 없이 어텐션만을 사용해 인코더-디코더 구조를 만들었다.

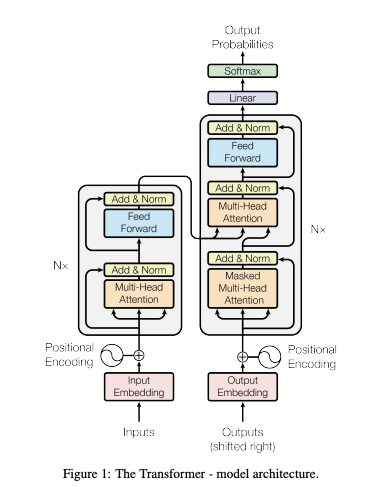
인코더와 디코더

인코더

• 인코더는 총 여섯 개의 층으로 쌓여져 있다

• 각 층은 두 개의 sub-layer를 가지고 있다. 첫 번째는 Multi-Head Attetion 층이고, 두 번째는 점별 완전 연결(point wise fully connected) Feed Forward 로 연결되어 있다.

• 두 개의 sub-layer에 각각 잔차 연결(residual connection)을 사용하며, 레이어 정규화(normalization)을 수행한다.

• 즉, 각각의 sub-layer의 output은 $\text{LayerNorm}(x + \text{Sublayer}(x))$이고, $\text{Sublayer}(x)$는 sub-layer에서 실행되는 함수다.

• 잔차 연결을 용이하게 하기 위해 모델의 모든 sub-layer 및 임베딩 레이어는 512개의 차원으로 output을 생성한다.

디코더

• 디코더 역시 총 여섯 개의 층으로 쌓여져 있다.

• 두 개의 sub-layer 외에도 인코더의 결과에 Multi-Head Attention을 수행할 세 번째 sub-layer를 추가한다.

• 인코더와 마찬가지로 두 개의 sub-layer에 각각 잔차 연결(residual connection)을 사용하며, 레이어 정규화(normalization)을 수행한다.

어텐션

Attention, 어텐션 포스트에 기술했듯, 특정 정보에 좀 더 주의를 기울이는 것이다. 또한 어텐션에는 다양한 계산 방법이 존재하는데, Transformer에서는 Scaled Dot-Product Attention(스케일드 닷-프로덕트 어텐션)을 사용한다.

스케일드 닷-프로덕트 어텐션

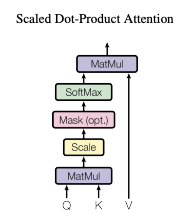
• 입력값은 Query와 차원 $d_k$의 Key, 그리고 차원의 값 $d_v$를 고려한다. Query와 모든 Key에 대해 내적(dot product) 계산을 하고, 각각 $\sqrt{d_k}$로 나눈 다음, 값에 대한 가중치를 구하기 위해 소프트맥스 함수를 적용한다.

• 동시에 쿼리 집합에 대해 어텐션 함수를 계산하고, 매트릭스 Q로 묶는다. Key와 Value들 또한 각각 K, V 매트릭스로 묶는다. 이를 다음과 같이 쓸 수 있다.

  \[\text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V\]

• 가장 많이 사용되는 두 가지 어텐션 함수는 addictive attention과 dot-product attention인데, 스케일드 닷-프로덕트 어텐션은스케일링 요소인 $\frac{1}{\sqrt{d_k}}$ 가 있다는 것만 제외하면 Dot-Product Attention과 동일하다.

• 소프트맥스를 거친 값을 value 에 곱해준다면, query와 유사한 value일수록 더 높은 값을 가지게 된다 -> 중요한 정보에 더 관심을 둔다!

멀티 헤드 어텐션

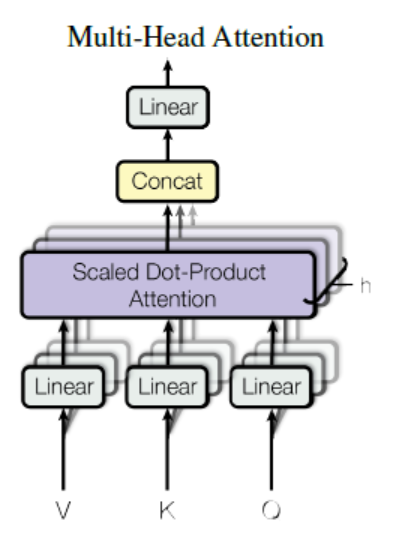
• $d_{model}$-dimensional Key, Value, Query을 가지고 단일 어텐션 함수를 수행하는 것 대신에, 각각 ${d_k}$, ${d_k}$, ${d_v}$ 크기에 대해 서로 다른 학습된 선형 투영(linear projection)을 사용해 h번 수행하는 것이 좋다고 한다.

• 즉 동일한 Q, K, V에 대해 각각 다른 parameter matrix인 W를 곱해주는 것.

  \[\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \cdots, \text{head}_h)W^o \\ \text{where } \text{head}_i = \text{Attention}(QW^Q_i, KW^K_i, VW^V_i)\]

• W는 각각

  \[W_i^Q \in \mathbb{R}^{d_{model} \mathsf{x} d_k} \\ W_i^K \in \mathbb{R}^{d_{model} \mathsf{x} d_k} \\ W_i^V \in \mathbb{R}^{d_{model} \mathsf{x} d_v} \\ W_i^O \in \mathbb{R}^{hd_ v\mathsf{x} d_{model}}\]

• 순서대로 query, key, value, output에 대한 parameter matrix이다.

• 여기서 8개의 head 또는 레이어를 병렬적으로 사용한다. 각각에 대해 $d_k = d_v = d_{model}/h = 64$를 사용한다. 각 head별로 차원 감소로 인해, 전체 계산 비용은 완전 차원을 가진 단일 어텐션과 유사하다.

어텐션 적용

트랜스포머는 멀티 헤드 어텐션을 세가지 다른 방법으로 사용한다.

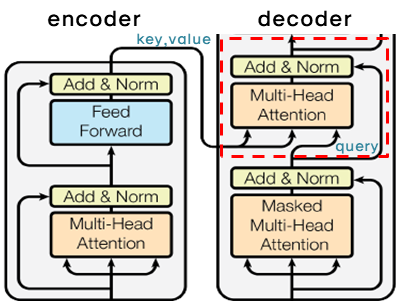
• “인코더-디코더 어텐션” 레이어는 Query가 이전의 디코더 레이어에서 오고, 메모리 Key와 Value는 인코더의 output으로부터 온다. 이렇게 하면 디코더의 모든 위치가 모든 position을 참조할 수 있다. -> 인코더의 output의 모든 position에 attention을 줄 수 있다.

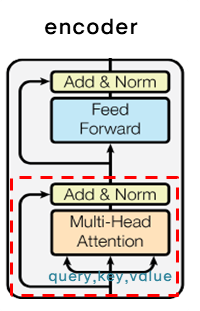
• 인코더는 셀프 어텐션 레이어를 포함한다. 셀프 어텐션의 모든 Key, Value, Query들은 인코더의 이전 레이어의 output에서 온다. 각각의 인코더 포지션은 인코더의 이전 레이어의 모든 position을 참조할 수 있다. -> 이전 레이어의 모든 position에 attention을 줄 수 있다!

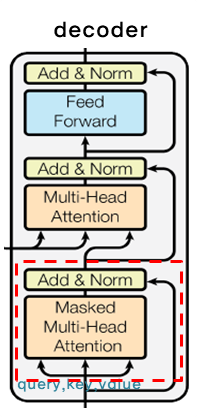
• 마찬가지로, 디코더의 셀프 어텐션 레이어는 디코더의 각 포지션을 해당 포지션까지 포함하여 모든 위치를 처리할 수 있도록 한다. auto-regressive 특성을 보존하기 위해 디코더에서 왼쪽으로 정보가 흐르는 것을 방지할 필요가 있다. -> i번 째 output을 다시 i+1번 째 input으로 사용하는 auto-regressive한 특성을 유지하기 위해, masking out된 스케일드 닷-프로덕트 어텐션을 적용한다.

점별 피드포워드 네트워크

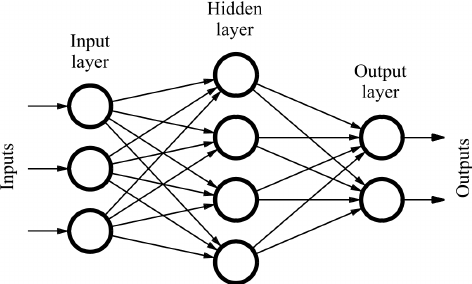
• 어텐션 sub layer에 이어, 인코더와 디코더 레이어 각각 완전 연결된 피드포워드 네트워크를 포함하는데, 이 네트워크는 각 position마다 개별적으로 그리고 동일하게 적용된다(separately and identically). -> position-wise

• 중간에 ReLU 활성화 함수가 있는 두 개의 선형 변환(linear transformation)으로 구성된다.

  \[\text{FFN}(x) = \text{max}(0, xW_1 + b_1)W_2 + b_2\]
  • 첫 번째 선형 변환: $f_1 = xW_1 + b_1$
  • ReLU: $f_2 = \text{max}(0, f_1)$
  • 두 번째 선형 변환: $f_3 = f_2W_2 + b_2$

• 선형 변환은 서로 다른 위치에 걸쳐 동일하게 적용되지만, 각각의 층마다 다른 매개변수를 사용한다. -> 커널 사이즈 1을 사용하는 두 개의 Convolution(CNN)이다.

  • input과 output의 차원 수 $d_{model} = 512$
  • inner layer의 차원 수 $d_{ff} = 2048$

임베딩과 소프트맥스

• 다른 시퀀스 전달(sequence transduction) 모델과 유사하게, input 토큰과 output 토큰을 $d_{model}$ 차원의 벡터로 변환하기 위해 학습이 되어있는 임베딩을 사용한다.

• 또한 통상적으로 학습된 선형 변환과 소프트맥스 함수를 사용하여 디코더 ouptut을 예측된 다음 토큰 확률로 변환한다.

• 모델은 두 개의 임베딩 레이어와 사전 소프트맥스 선형 변환 사이에 같은 가중치 매트릭스를 공유한다. 임베딩 레이어는 $\sqrt{d_{model}}$ 을 곱해준다.

포지셔널 인코딩

• 트랜스포머는 recurrence와 convolution을 포함하지 않기 때문에, sequence 순서를 사용하기 위해 순서대로 토큰의 상대적/절대적인 position에 대한 정보를 주입해야만(must!) 한다. -> 각 단어별로 position에 대한 정보를 추가해주겠다는 뜻

• 이를 위해, 인코더와 디코더 스택의 맨 밑(트랜스포머 모델 그림 참조)에 있는 “input embedding”에 “포지셔널 인코딩(positional encoding)”을 추가한다.

• 포지셔널 인코딩은 $d_{model}$(임베딩 차원)과 같은 차원을 같기 때문에 포지셔널 인코딩과 임베딩 벡터는 더해질 수 있다.

• 논문에서는 다른 frequncy(주어진 구간 내에서 완료되는 사이클의 개수)를 가지는 사인함수와 코사인함수를 이용했다.

  \[\text{PE}_{(pos, 2i)} = sin(pos/10000^{2i/d_{model}})\] \[\text{PE}_{(pos, 2i + 1)} = cos(pos/10000^{2i/d_{model}})\]

• pos: 포지션, i = 차원. 즉, 포지셔널 인코딩의 각 차원은 사인곡선(sinusoid)에 부합한다. 주기는 $10000^{2i/d_{model}} \cdot 2\pi$ 인 삼각함수. -> pos는 sequence에서 단어의 위치이고 해당 단어는 i에 0부터 $d_{model}/2$까지를 대입해 $d_{model}$차원의 포지셔널 인코딩 벡터를 얻게 된다.

• 짝수일 때는 사인함수, 홀수일 때는 코사인 함수를 이용. 이렇게 포지셔널 인코딩 벡터를 pos마다 구한다면 비록 같은 column일지라도 pos가 다르다면 다른 값을 가지게 된다!

• 논문에서는 학습된 포지셔널 임베딩 대신 sinusoidal version을 선택했다. 만약 학습된 포지셔널 임베딩을 사용할 경우 training보다 더 긴 sequence가 inference시에 입력으로 들어온다면 문제가 되지만 sinusoidal의 경우 일정하기 때문에 문제가 되지 않습니다. 그냥 좀 더 많은 값을 계산하기만 하면 된다.

왜 셀프어텐션?

• 이번 section에서는 셀프 어텐션 레이어들과 순환(recurrent) 그리고 convolution 레이어들을 비교한다. 비교 방법은 symbol representations(x1, …, xn)의 one variable-length sequence를 같은 길이 (z1, …, zn)으로 mapping 이다. 우리가 self-attetion을 사용하는 이유는 세 가지이다.

• 첫 번째는 레이어 별 총 연산의 복잡성. 두 번째는 sequential 연산에 최소로 얼마나 필요한지 측정된 병렬 처리 연산량.

• 세 번째는 네트워크에서 long-range dependencies 사이 path length이다. long-range dependencies의 학습은 번역 업무에서 key chanllenge(핵심 도전)이다. 이러한 dependencies을 학습하는 능력에 영향을 미치는 한 가지 핵심 요소는 전달해야 하는 forward 및 backward signal의 길이. input의 위치와 output의 위치의 길이가 짧을수록 dependencies 학습은 더욱 쉬워진다. 그래서 서로 다른 layer types로 구성된 네트워크에서 input과 output 위치 사이 길이가 maximum 길이를 비교한다. -> 단어와 단어 사이가 길 때 얘가 얼마나 잘 기억하냐!

• 위 표에 적혀있듯이, 하나의 셀프 어텐션 레이어는 연속적으로 수행되는 연산 수의 모든 포지션을 연결한다. 반면에 순환 레이어는 $O(n)$ 만큼의 순차 작업이 필요하다.

• 연산 복잡도 면에서 셀프 어텐션 레이어는 시퀀스가 반복될 때 순환 레이어보다 빠르다. 길이 n은 차원 d보다 작으며, 이는 word-piece나 byte-pair 표현과 같은 기계 번역에서 최첨단 모델이 사용하는 문장 표현에 해당한다.

• 매우 긴 시퀀스를 포함하는 작업에 대한 계산 성능을 개선하기 위해, 셀프 어텐션은 각 출력 위치를 중심으로 한 입력 시퀀스에서 이웃된 r 크기만을 고려하는 것만으로 제한될 수 있다. 이렇게 하면 최대 경로 길이가 $O(n/r)$ 로 증가한다. 이건 추후에 조사할 계획이다.

• 커널 길이 k가 n보다 작은 단일 convolutional 레이어는 모든 input과 output 포지션 쌍을 연결하지 않는다. 연결시키기 위해서는 연속적인 커널의 경우 $O(n/k)$의 convolutional 레이어를 쌓거나, 확장된 convolution의 경우 $O(log_k(n))$ 만큼 쌓아야 하며 네트워크의 어떤 두 포지션 사이의 가장 긴 경로의 길이를 증가시킨다.

• convolution 층은 일반적으로 순환 층보다 k의 비율로 계산량이 비싸다. 그러나 분리가능한 convolution의 경우, 복잡도는 $O(k \cdot n \cdot d + n \cdot d^2)$ 만큼 상당히 감소한다. k = n이어도 분리 가능한 convolution의 복잡도는 트랜스포머에서 사용하는 접근방식인 셀프어텐션과 점별 피드포워드 레이어의 결합과 같다.

• 추가로 얻는 이익으로서, 셀프 어텐션은 더 많은 해석 가능한 모델을 산출할 수 있다.

훈련

Optimizer

• adam 을 사용했으며 $\beta_1 = 0.9$, $\beta_2 = 0.98$ 그리고 $\epsilon = 10^{-9}$를 사용했다.

• 학습 비율(learning rate)은 가변적으로 변한다.

  \[lrate = d_{model}^{-0.5}\cdot min(step\_num^{-0.5},step\_num \cdot warmup\_steps^{-1.5})\]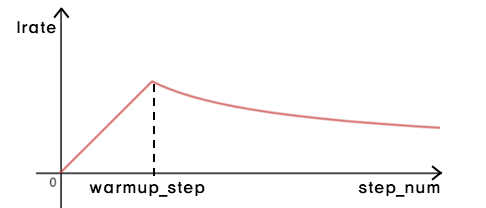

  

• warmup_step까지는 linear하게 learning rate를 증가시키다가 warmup_step 이후에는 step_num의 inverse square root에 비례하도록 감소시켰다. 여기서 warmup_step = 4000 사용했다.

정규화

잔차 드롭아웃

각 sub-layer의 output에 드롭아웃을 적용하고, sub-layer input에 추가하여 normalize한다. 또한 인코더 스택과 디코더 스택의 임베딩 및 포지셔널 인코딩의 합에 드롭아웃을 적용했다. 모델에서 드롭아웃 비율은 0.1로 설정했다.

라벨 스무딩

라벨 스무딩 논문 참고

훈련하는 동안, 라벨 스무딩을 적용했다. $\epsilon_{ls} = 0.1$. 이것은 모델이 더 확실하지 않다는 것을 학습하면서 혼란을 주지만 정확성과 BLEU 점수를 향상시킨다.

결론

• 본 연구에서는, 인코더 디코더 아키텍처에서 가장 일반적으로 사용되는 순환 레이어를 멀티 헤드 셀프 어텐션으로 대체하면서, 전적으로 어텐션만을 사용한 최초의 시퀀스 변환 모델인 Transformer를 제시했다.

• 번역 과제의 경우, 트랜스포머는 순환 또는 convolutional 레이어에 기반한 구조보다 훨씬 빠르게 훈련될 수 있다.